通常の行列は、要素に数字や文字が入っています。その要素がすべて0(ゼロ)で構成された行列を、特別にゼロ行列と呼び、0(オー)で表します。
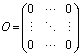
このとき、行列の型は何×何になっていようが構いません。すべての要素がゼロであればゼロ行列と呼びます。
授業内容
行列の掛け算
行列の掛け算を行うために、さらに、ちょっとだけ知識を追加しましょう。
ゼロ行列
![]()
通常の行列は、要素に数字や文字が入っています。その要素がすべて0(ゼロ)で構成された行列を、特別にゼロ行列と呼び、0(オー)で表します。
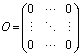
このとき、行列の型は何×何になっていようが構いません。すべての要素がゼロであればゼロ行列と呼びます。
正方行列
行の数と列の数が等しい、すなわち、n×n行列になっているとき、n次の正方行列と呼びます。
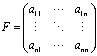
また、正方行列の対角線上、つまり、![]() 座標に並んだ成分のことを対角成分と呼び、対角成分以外の要素がすべてゼロになっている行列のことを、対角行列と呼びます。
座標に並んだ成分のことを対角成分と呼び、対角成分以外の要素がすべてゼロになっている行列のことを、対角行列と呼びます。
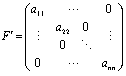
単位行列
対角行列の対角要素がすべて1で構成されているものを単位行列と呼び、E やI で表現します。
この単位行列は、行列の世界での1にあたると考えてもらえばいいと思います。
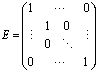
次数を明確にしたい場合、特に、![]() と表現することがあります。
と表現することがあります。
転置行列
行列Aの行と列を入れ替えたものを、行列Aの転置行列と言い、![]() で表します。すると、行列Aがn×m行列だった場合、行列
で表します。すると、行列Aがn×m行列だった場合、行列![]() はm×n行列になります。
はm×n行列になります。
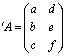
行列の掛け算
行列の掛け算はちょっと特殊になります。まず、A×Gという計算を行いたいとき、行列Aの列と行列Gの行の数が一致していなければいけません。
![]() 、
、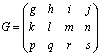
例えば、Gが上のような3×4行列であれば、掛け算が可能になります。
注意しなければならないのは、行列の掛け算の場合通常の数字(スカラー)のような交換則が成り立たない点です。つまり、掛け算を行う場合、行列Aに対し行列Gを右から掛けるのか、左から掛けるのかが重要の意味を持ってくるのです。
![]() (例外あり)
(例外あり)
また、その場合次のような手順で計算を実行します。
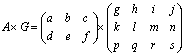
![]()
つまり、2×3行列に右から3×4行列を掛けると、2×4行列が出来上がります。
下線の部分が一致していることが重要です。その意味で、3×4行列に、右から2×3行列を掛けることはできません。また、n次の正方行列F,F’がある場合、F×F’とF’×Fの両方が定義できますが、解が一致する保証はありません。
【新規プログラム1先頭】
proc iml;
reset print;
A = {1 2 3,4 5 6};
G = {7 8,9 0,1 2};
AG = A * G;
GA = G * A;
quit;
【新規プログラム1末尾】
成り立たないはずの交換則の例外が、正方行列と単位行列の掛け算です。
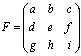 、
、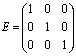
すると、
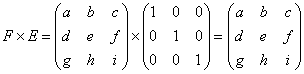
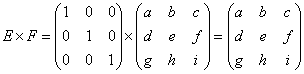
どちらも同じ結果が得られます。
もう一つの例外が次の「逆行列」の概念です。
n次の正方行列Jに対して、
![]()
を満たすn次正方行列Kが存在するとき、JとKは可換であると言います。またその際、次の関係が成り立つとき、KをJの逆行列と言い![]() (Jのインバース)で表します。
(Jのインバース)で表します。
![]()
ただし、Eはn次の単位行列です。
行列の割り算
行列には、割り算という概念はありません。そこで、上で使った逆行列による掛け算によって、割り算にあたる操作を行います。
![]()
この関係から、Lを取り出すためには次のような処理を行います。両辺の右から(結構重要)Mの逆行列を掛けると、
![]()
![]()
![]()
として、Lを取り出すことができます。(Mを取り出す場合には、Lの逆行列を両辺の左から掛けます)
逆行列は次のようにして表します。
【新規プログラム2先頭】
proc iml;
reset print;
L = {2 -1, -1 2};
M = {1 1, 1 -1};
invL = inv(L);*invは先のインバースの意味;
E = L * invL;
quit;
【新規プログラム2末尾】
上のプログラムのLとMはともに逆行列を持つが、そのとき以下の等式が成り立つのを確かめなさい。
LとMの位置に注意すること。