一次変換による図の移動

c = {{0, 0}, {19, 10}, {0, 10}, {16, 0}, {9, 15}};

Showを使って確認してみましょう。

Show[Graphics[Polygon[c]], AspectRatio -> Automatic];

この図を一次変換という手法を使って動かすことを考えてみます。

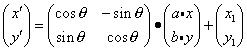
これは、という座標にある点を、という座標に移すための式になっています。それぞれ、どのような意味になっているかを考えてみましょう。

平行移動

平行移動は、単純な座標の移動を意味するので、次のような式で表現することができます。

a = 1; b = 1; t = 0/180*Pi; x1 = 10; y1 = 10;
f[{x_, y_}] := {{Cos[t], -Sin[t]}, {Sin[t], Cos[t]}}.{a*x, b*y} + {x1, y1};
Show[Graphics[{GrayLevel[0.5], Polygon[Map[f, c]],
GrayLevel[0], Polygon[c]}], AspectRatio -> Automatic];

拡大・縮小

図のサイズを変えたいと思ったときには、ｘ方向、ｙ方向にそれぞれ何倍の大きさにしたいかを考える必要があります。下は、単純に３倍の大きさにするための式です。

a = 3; b = 3; t = 0/180*Pi; x1 = 0; y1 = 0;
f[{x_, y_}] := {{Cos[t], -Sin[t]}, {Sin[t], Cos[t]}}.{a*x, b*y} + {x1, y1};
Show[Graphics[{GrayLevel[0.5], Polygon[Map[f, c]],
GrayLevel[0], Polygon[c]}], AspectRatio -> Automatic];

回転

ここではθという回転角の代わりに、ｔ　を使ってその大きさを表現しています。下は、原点(0,0)を軸にして、180度回転させるための式です。

a = 1; b = 1; t = 180/180*Pi; x1 = 0; y1 = -1;
f[{x_, y_}] := {{Cos[t], -Sin[t]}, {Sin[t], Cos[t]}}.{a*x, b*y} + {x1, y1};
Show[Graphics[{GrayLevel[0.5], Polygon[Map[f, c]],
GrayLevel[0], Polygon[c]}], AspectRatio -> Automatic];

複合

星に影が付いて、それが伸びているような表現をしたいとき、次のように書くといいでしょう。

Clear[f, b, x, a]
m = {{1, 1}, {0, -b}}; b = 3;
f[x_List] := m.x;
Show[Graphics[{GrayLevel[0.5], Polygon[Map[f, c]], GrayLevel[0], Polygon[c]}],
AspectRatio -> Automatic];

アニメーション

では、その影が伸びていくようなアニメーションを作ってみましょう。

Clear[f, b, x, a]
m = {{1, 1}, {0, -b}}; b = 3;
f[x_List] := m.x;
Do[Show[Graphics[{GrayLevel[0.5], Polygon[Map[f, c]], GrayLevel[0],
Polygon[c]}, PlotRange -> {{-3, 40}, {-80, 20}}],
AspectRatio -> Automatic], {b, 2, 5, 0.1}];

回転のアニメーション

前回までの応用で、星を原点を中心に回転させるような式を考えて見ましょう。

a = 1; b = 1; t = i; x1 = 0; y1 = 0;
f[{x_, y_}] := {{Cos[t], -Sin[t]}, {Sin[t], Cos[t]}}.{a*x, b*y} + {x1, y1};
Do[Show[Graphics[{GrayLevel[0.5], Polygon[Map[f, c]],
GrayLevel[0], Polygon[c]}], AspectRatio -> Automatic], {i, 0, 2Pi, Pi/16}];

鏡面移動（線対称）

回転は、点対称な移動を意味しています。線対称にしたいときには次のように書けばそれができます。下は、縦軸に対して対称にしています。横軸に対称にしたり、斜めに対称にしたいとき、どうすればいいか考えてみてください。

a = 1; b = 1; t = 0/180*Pi; x1 = 0; y1 = 0;
f[{x_, y_}] := {{-1, 0}, {0, 1}}.{a*x, b*y} + {x1, y1};
Show[Graphics[{GrayLevel[0.5], Polygon[Map[f, c]],
GrayLevel[0], Polygon[c]}], AspectRatio -> Automatic];