Mathematicaを使ったミクロ経済学の効用最大化問題
次のような効用関数が与えられていたとしましょう。対数関数で表現されていますが、以前実験したコブダグラス型の関数が原型です。
u[x1_ , x2_ , a_ ] := a*Log[x1] + (1 - a)*Log[x2]
意味は、(1) u という関数を設定する。(2)変数として、x1、x2、a を含む。と、なります。
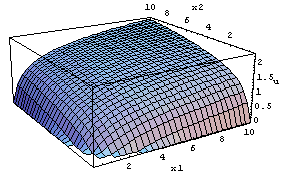
これを、まず、立体的なグラフで見るためには次のように表現します。
objective = Plot3D[
u[x1, x2, 0.5], {x1, 0.01, 10} , {x2, 0.01, 10},
AxesLabel -> {"x1", "x2", "u"},
ViewPoint -> {-1.7, -2.7, 1.1},
PlotPoints -> 30,
PlotRange -> {0, Automatic},
ClipFill -> None]

関数とその範囲、軸の名前、視点の位置、描画の大きさ、範囲を指定しています。<練習1>等高線で表現するときにはどうやっていたか試してみましょう。
次に、次のような面で、このグラフを縦に切ってみます。
x1 + 1.5 x2 = 6
そのための表現は次のようになります。
constraint = ParametricPlot3D[
{x1, 4 - x1/1.5, u},
{x1, 0, 6}, {u, 0, u[10, 10, 0.5]},
ViewPoint -> {-1.7, -2.7, 1.1},
PlotPoints -> 30]
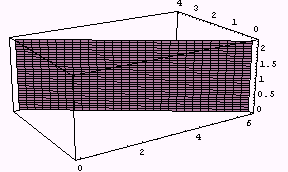
この二つを合成してみましょう。
Show[objective, constraint]
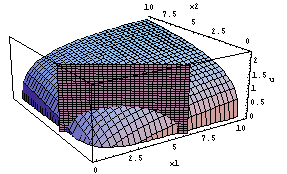
この面の最高の値が、そのときに達成できる最高の効用水準となります。
多少辛いでしょうが、数学的にこの問題を解いて見ましょう。
「予算の制約の下での効用最大化」問題というのは次のように表現することができます。これをラグランジュ方程式と呼びます。
L = u[x1, x2, a] + lambda*(m - p1*x1 - p2*x2)
この、x1、x2について微分することで最適解を求めてやります。
foc = {D[L, x1] == 0, D[L, x2] == 0, D[L, lambda] == 0}
そこで得られた解を、表示しましょう。
sol = Solve[foc, {x1, x2, lambda}][[1]]
計算を実行すると次のようになります。
xm1[ p1_, p2_, m_ ] := Evaluate[Simplify[x1 /. sol]]
xm2[ p1_, p2_, m_ ] := Evaluate[Simplify[x2 /. sol]]
xm1[ p1, p2, m ]
xm2[ p1, p2, m ]
次に予算の制約は次のように書くことができます。
g[x1_, x2_] := p1*x1 + p2*x2 - m
各値を次のように設定してやります。
p1 = 1.5 ; p2 = 1.0 ; m = 6.0 ; a = 0.5;
それぞれの値を代入して均衡点を求めると次のように書くことができます。
xm1[ p1, p2, m ]
xm2[ p1, p2, m ]
次に、これを図示することで求めてみましょう。まず、効用関数は次のようにかけます。
cp1 = ContourPlot[u[x1, x2, a], {x1, 1, 10}, {x2,
1, 10},
Contours -> {u[xm1[p1, p2, m], xm2[p1, p2, m], a]},
ContourShading -> False, DisplayFunction -> Identity]
さらに、予算線。
cp2 = ContourPlot[g[x1, x2], {x1, 1, 10}, {x2, 1,
10},
Contours -> {g[xm1[p1, p2, m], xm2[p1, p2, m]]},
ContourShading -> False, DisplayFunction -> Identity]
次いで、均衡点を表示してやります。
tE = Show[Graphics[Text["E", {xm1[p1, p2, m] +
0.2, xm2[p1, p2, m] + 0.2}]],
DisplayFunction -> Identity]
この3つを合成して、最適点を表示してやります。
Show[cp1, cp2, tE,
FrameLabel -> {"x1", "x2"},
PlotLabel -> "Optimal Choice", DisplayFunction ->
$DisplayFunction]
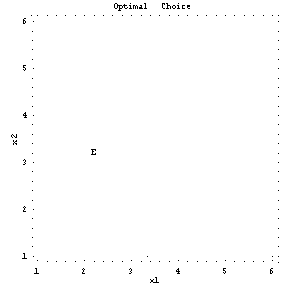
実際、x1、x2、a がそれぞれ、2、3、0.5の場合、効用水準は次のように求められます。
un = N[u[2, 3, 0.5]]
ここで、そのときの選ばれた無差別曲線が最適であるという事をアニメーションで見てみましょう。
式1
region = ContourPlot[g[x1, x2], {x1, 0, 10}, {x2,
0, 10},
Contours -> {0},
ContourShading -> False,
FrameLabel -> {"x1", "x2"},
PlotLabel -> "予算制約の下での効用最大化問題",
DisplayFunction -> Identity]
式2
objectives = Table[
ContourPlot[u[x1, x2, 0.5], {x1, 0.01, 10}, {x2, 0.01, 10},
Contours -> {t},
ContourShading -> False,
DisplayFunction -> Identity], {t, un - 0.3, un + 0.3, 0.1}]
式3
Table[Show[region, objectives[[n]],
DisplayFunction -> $DisplayFunction], {n, 1, 7}]