Plot3D[x^0.4 y^0.6, {x, 0, 100}, {y, 0, 100}]
授業内容
算術演算
足し算 +
引き算 −
掛け算 *
割り算 /
べき乗 ^
では、198と195という二つの数字の算術演算をしてみましょう。例えば、足し算は
198+195
と入力した後で、「Shift + Enter」で計算が実行されます。特徴的なのは、掛け算と割り算です。まず、
198*195
を実行してみてください。次に、
198 195
を実行してください。同じ結果が得られます。僕たちが通常使うように(例えば、2×Aを2・Aと書くように)スペースによって掛け算を省略しても構わないわけです。次に、割り算ですが、
198/195
を実行してみましょう。答えは分数で出てきます。不正確な小数での表現ではなく、分数を使うことで表現可能なものは分数で表してくれます。
また、”%”を使うことで、直前の計算結果をそのまま引用することも可能です。
% 2
変数の定義も簡単に作れるようになっています。次のように順番に入力して実行してみましょう。
test=198 (実行)
test1=195 (実行)
test2=45 (実行)
そこで次のように打って実行します。
test*test1/test2
ここで注意しなければならないのは、test2 と test 2 を間違えて入力しないことです。test2は1つの変数ですが、test 2 は2倍のtestになってしまいます。このような、機能を持つMathematicaを使って、グラフを描いたり、写像を作ったりすることを考えていきます。
3次元で表現
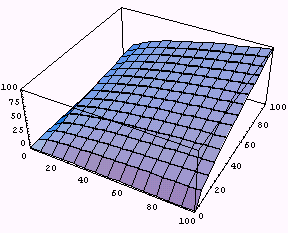
Plot3D[x^0.4 y^0.6, {x, 0, 100}, {y, 0, 100}]
等高線として表現
ContourPlot[x^0.4 y^0.6, {x, 0, 100}, {y, 0, 100}]
Plot3D、ContourPlot ともに立体を表現するための関数です。そこで、関数の形状を表すとともに、その範囲を指定してやることで、関数の雰囲気を掴むことができるようになります。経済学では、消費量x、yともに正の値として扱うのが通常なので、ここでは上のような範囲の指定を行っています。
まず、初めに2次元での描画からはじめていきましょう。
Plot
Plot には2つの引数が存在します。1つ目は、関数、または関数のリストがきます。2つ目が反復子(iterator)になります。
Plot[ 関数(のリスト) , 反復子 ] ;
実際次のように書いて見ましょう。
Plot[Sin[ x ] , { x , 0 , 2 Pi } ] ;
Sin は組み込み関数のサインカーブです。2項目の { x , 0 , 2 Pi } が反復子と呼ばれるもので、ここでは、x の範囲を指定しています。反復子の中にある Pi は円周率πのことを表していて、ゼロから2πの範囲を指定することで、サインカーブを1周期動かしているわけです。
変数は、1つに限ったわけではありません。次のように複数のリストとして書くことも可能です。ブレス{ }でくくった値のことをリストと呼んでいます。Mathematicaでは、行列やベクトルといった要素の集合を表すときに、このリストを用います。
Plot[ { Sin[ x ] , -Sin[ x ] , Cos[ x ] , -Cos[ x ] } , { x , 0 , 2 Pi } ] ;
また、様々なオプションを用いることで、より内容の濃い描画が可能になります。
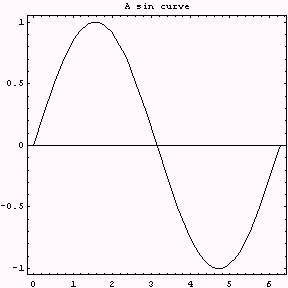
例1 枠を作って、タイトルを入れる
Plot[Sin[ x ] , { x , 0 , 2 Pi } ,
AspectRatio -> 1 ,
Frame -> True ,
PlotLabel -> " A sin curve "] ;
結果
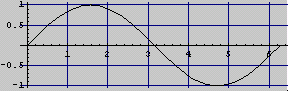
例2 背景をグレーにして、グリッドラインを入れる
Plot[Sin[ x ] , { x , 0 , 2 Pi } ,
AspectRatio -> Automatic ,
Background -> GrayLevel [0.8] ,
GridLines -> Automatic] ;
結果
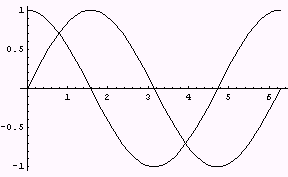
次に複数のグラフの合成を考えてみましょう。サイン曲線と別個に描いて、 Showというコマンドで合成することが可能です。
Show [ Plot[ Sin[ x ] , { x , 0 , 2 Pi } ] , Plot[ Cos[ x ] , { x , 0 , 2 Pi } ] ] ;
このとき、グラフは3つ作成されてしまいますが、その途中経過を表示するかしないかを決定するオプションが、DisplayFunctionです。 「Identity」と入れた場合、表示されません。
Show [ { Plot[ Sin[ x ] , { x , 0 , 2 Pi } , DisplayFunction -> Identity ] ,
Plot[ Cos[ x ] , { x , 0 , 2 Pi } , DisplayFunction -> Identity ] } ,
DisplayFunction -> $DisplayFunction ] ;
ListPlotは、基本的には座標を指定した点を描画するための命令文です。
ListPlot[ { 3.2 , 5.1 , 1.4 , 0.5 , 4.4 } , PlotStyle -> {PointSize[0.02] } ];
ここに、オプションとして点を結ぶ命令を加えてやるのが、「PlotJoined」です。デフォルト(指定なし)の場合は、Falseになっています。つまり、このままでは何も描かれないので、Trueの指示を入れて、直線でつないでやることにします。
ListPlot[ { 3.2 , 5.1 , 1.4 , 0.5 , 4.4 } ,
PlotRange -> { { 0 , 6 } , { 0 , 6 } } ,
AspectRatio -> 1 ,
PlotJoined -> True];
次に、関数で導かれる点の軌跡を追いかけて見ましょう。
data = Table[ N [ { x , Sin [ x ] } ] , { x , 0 , 2 Pi , Pi/5} ] ;
前回のサイン関数をπ/5ごとに座標を取る関数が上になります。ただし、これを実行しても何も表示されません。この式は、定義を行っているのだと理解してください。ListPlotを使って描画すると次になります。
ListPlot[ data , PlotStyle -> { PointSize[0.04]} , PlotRange -> { -1.1 , 1.1} ] ;
dataの式の結果は、保存しない限りデータとしては使用の制限を受けてしまいます。そこで次のようにして、結果だけをデータとして保存してやりましょう。
Put[OutputForm[data] , "storage"] ;
これを引き出して使うには、次のような操作が必要です。
ListPlot[ Get[ "storage"] , PlotStyle -> {PointSize[0.04] } , PlotRange -> { -1.1 , 1.1} ] ;
PutとGetの関係を覚えておきましょう。Putで一旦置いた物を、Getで取り出してくると理解すればいいでしょう。
さて、この点の流れは、3次関数のようにも見えるのですが、ここでdataの範囲を使って3次関数を描くfitCurveという変数を定義してみましょう。
fitCurve = Fit[ data , { 1, x , x^2 , x^3 } , x ] ;
前回試したPlotを使って、 これも前回使ったShowファンクションによる合成で、3次関数と点の軌跡の合成をやると次のような式を作ることが可能です。
Show [ Plot [fitCurve , { x , -0.5 , 6.7} , DisplayFunction -> Identity ] ,
ListPlot[ data , PlotStyle -> { PointSize[0.04]} ,
DisplayFunction -> Identity ] ,
DisplayFunction -> $DisplayFunction ] ;
ParametricPlot
次のような式を入力してみましょう。
ParametricPlot[{Sin[2 t], Sin[3 t]}, {t, 0, 2 Pi}]
これは、媒介変数という考え方です。x と y が、それぞれ x = sin(2t) , y = sin(3t)で表されるときに、t が動いたらどうなるかを表したグラフになります。いろいろな関数を代入して試してみましょう。
Plot3D
Plot3Dは、グラフを立体的に描くためのツールです。次のグラフを描いてみましょう。
Plot3D [ Cos[ x y ] , { x , 0 , Pi } , { y , 0 , Pi } , AxesLabel -> { "x-axis" , "y-axis" , "z-axis" } , AspectRatio -> 1 ] ;
Plot3D[2 Cos[ x y ] , { x , - Pi, Pi } , { y , 0 , Pi } , FaceGrids -> { { -1 , 0 , 0 }, { 0 , 1 , 0 } , { 0 , 0 , -1 } } , PlotPoints -> 40 ] ;
ParametricPlot3D
ParametricPlot3Dは、3次元空間内のパラメータ表示化された曲面や曲線を作図する。
ParametricPlot3D[{Sin[t] , Cos[t] , Sin[t]^2 } , { t , 0 , 2 Pi } , Axes -> False , BoxRatios -> { 1 , 1 , 1 } ];
ParametricPlot3D[{ r Cos[omega] , r Sin[omega] , omega/6 } , { r , 0 , 1 } , { omega , - Pi , 4 Pi } , PlotPoints -> {8 , Floor[ N [ 16 Pi] ] } , Boxed -> False , Axes -> False ];
ParametricPlot3D[{r Cos[t] , r Sin [t] , r^2 Cos[2 t] } , { t , 0 , 2 Pi } , { r , 0 ,1 } , Axes -> False , BoxRatios -> { 1 , 1 , 1 } , FaceGrids -> { { -1, 0 ,0 },{ 0 ,1 , 0 } , { 0 , 0 , -1}} , PlotPoints -> 40 ];
最初の方の授業で効用関数を描くときに使用したコマンドContourPlotも同様に描画のためのものでした。
アニメーションは、ノートブックフロントエンド環境で、Doループを用いて式の列を評価し、単純な反復子をコントロールすることで簡単に作成できます。基本的には、パラパラアニメと思ってください。
次の式は、振動する弦を書くための記述です。−2から6までの区間で次のような式を評価しよう。
shape[ x_ ] := x/4 /; 0 <= x < 1;
shape[ x_ ] := ( 2 - x)/4 /; 1 <= x < 2;
shape[ x_ ] := - shape[ - x ] /; x < 0
shape[ x_ ] := - shape[ x - 2 ] /; 2 <= x
Plot[ {0.3, -0.3, shape[x]}, {x, -2, 6}, AspectRatio -> Automatic, Ticks -> None];
時刻 t を関数とした弦の位置を次の2変数の関数で表す。
string[x_, t_] := 0.5 (shape[x - t] + shape[x + t])
今、時間区間を0から2としたときの弦の位置を11個の図によって表してみましょう。
Do [Plot[Evaluate[{0.3, -0.3, string[x, 0.2 t]}], {x, 0, 2}, Ticks -> None , PlotRange -> All], {t, 0, 10}];
この形では、場所とメモリーを食ってしまうので、一枚絵にして見るようにしましょう。
Show[GraphicsArray[Table[Plot[{0.3, -0.3, Evaluate[string[x, 0.2 (4 i + j)]]}, {x, 0, 2}, Ticks -> None, PlotRange -> All , DisplayFunction -> Identity], {i, 0, 2}, {j, 0, 3}]], DisplayFunction -> $DisplayFunction];
サウンド
サウンドの作成は、図と全く同じように行われる。下のプログラムは、サインカーブを指定し、Playコマンドによってその曲線を「表示」している。
Play[{Cos[440 2 Pi t] , Sin[440 5/4 2 Pi t] , Sin[440 3/2 2 Pi t]}, {t, 0, 2}];